������ƪ���������ǽ����˾���������Ļ���ԭ������������������Ķ��塢�������ȡ�������Ҫд������������ν���һ��������ѵ��������ǰ���ͷ��������Լ���дһ�����������硣������˽����ԭ���ģ������ȿ�����ƪ���£������ѧϰϵ�С�����������CNNԭ�����(һ)��������ԭ��
�����������ǰ��
����������������һ����ľ��������磺
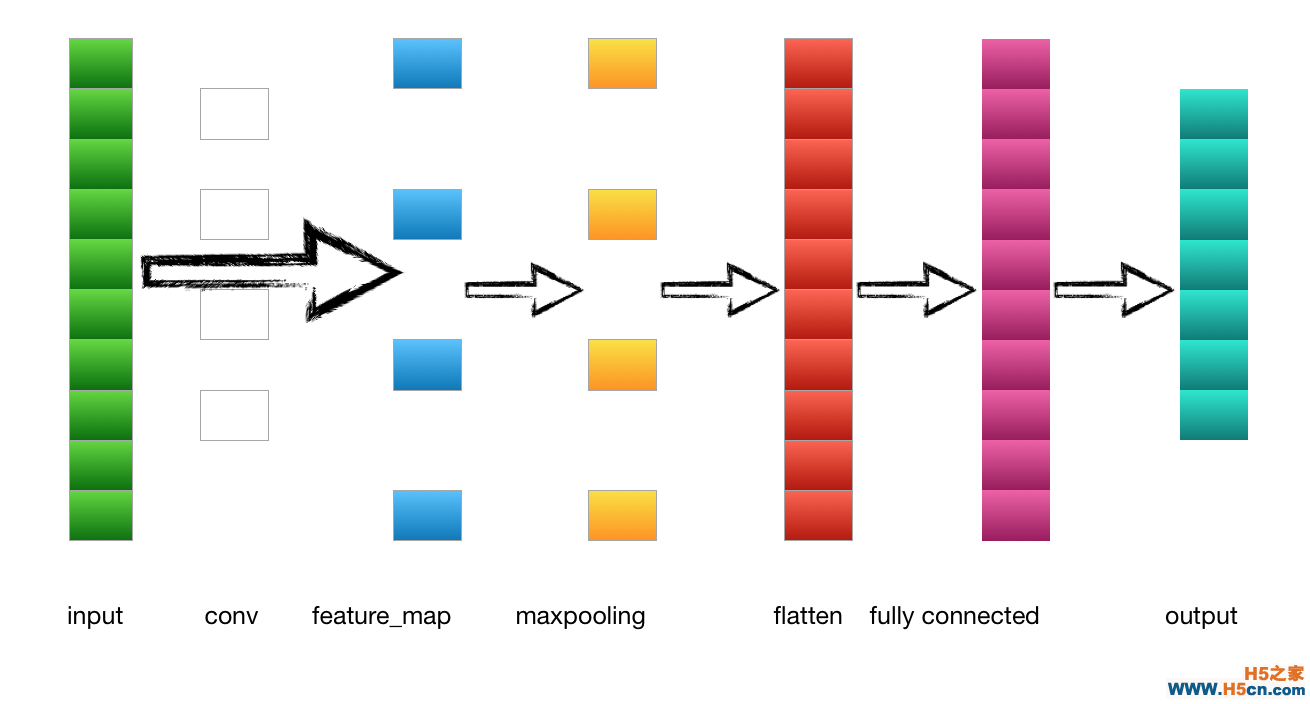
��1.�����---->������
��������һ�ڵ�����Ϊ����������һ��4*4 ��image����������2*2�ľ����˽��о�������������3*3��feature_map
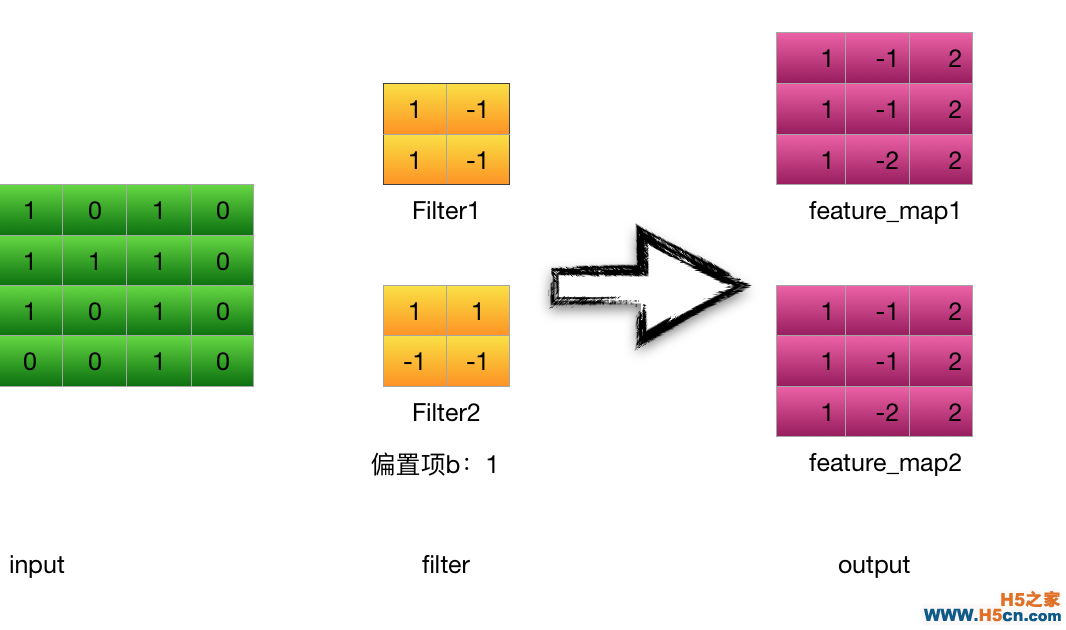
�����Ծ�����filter1Ϊ��(stride = 1 )��
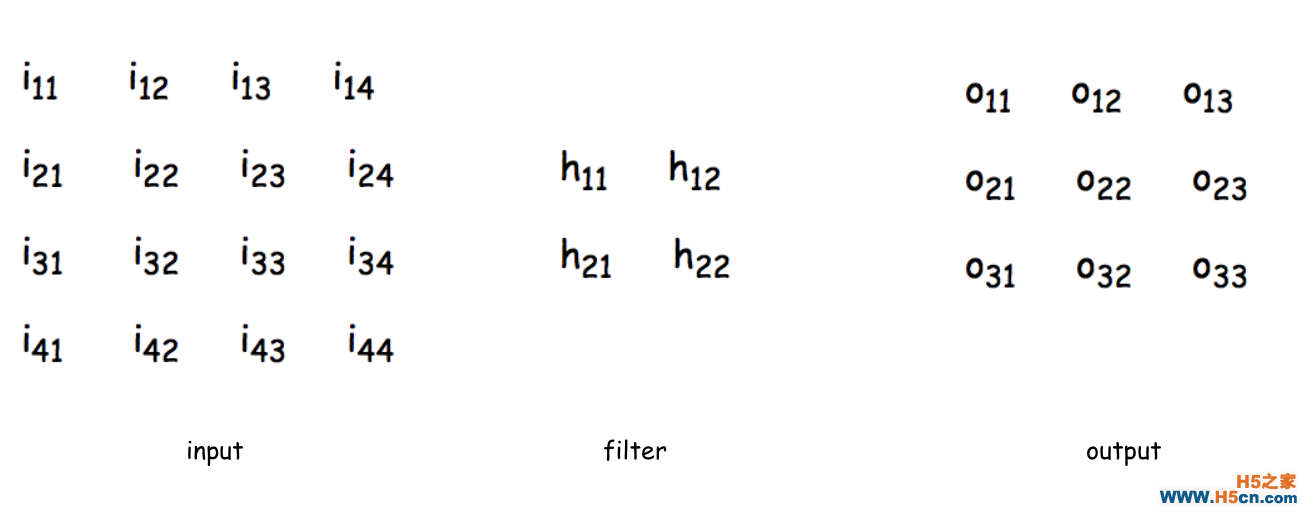
���������һ����������Ԫo11������:��
\begin{equation}
\begin{aligned}
\ net_{o_{11}}&= conv (input,filter)\\
&= i_{11} \times h_{11} + i_{12} \times h_{12} +i_{21} \times h_{21} + i_{22} \times h_{22}\\
&=1 \times 1 + 0 \times (-1) +1 \times 1 + 1 \times (-1)=1
\end{aligned}
\end{equation}
������Ԫo11�����:(�˴�ʹ��Relu�����)
\begin{equation}
\begin{aligned}
out_{o_{11}} &= activators(net_{o_{11}}) \\
&=max(0,net_{o_{11}}) = 1
\end{aligned}
\end{equation}
����������Ԫ���㷽ʽ��ͬ
��2.������---->�ػ���
����

��������ػ���m11 ������(ȡ����Ϊ 2 * 2),�ػ���û�м��������
\begin{equation}
\begin{aligned}
net_{m_{11}} &= max(o_{11},o_{12},o_{21},o_{23}) = 1\\
&out_{m_{11}} = net_{m_{11}} = 1
\end{aligned}
\end{equation}
����3.�ػ���---->ȫ���Ӳ�
�����ػ���������flatten�������Ԫ�ء���ƽ����Ȼ��ȫ���Ӳ㡣
����4.ȫ���Ӳ�---->�����
����ȫ���Ӳ㵽����������������Ԫ����Ԫ֮����ڽ�������ͨ��softmax��������������output���õ���ͬ���ĸ���ֵ���������ֵ���ļ�Ϊ��ͼƬ�����
����������ķ���
������ͳ����������ȫ������ʽ�ģ�������з�����ֻ��Ҫ����һ���ǰһ�㲻�ϵ���ƫ����������ʽƫ���Ϳ������ÿһ�����������Ȼ�����Ȩ�غ�ƫ������ݶȣ����ɸ���Ȩ�ء�����������������������IJ㣺������ͳػ������ػ������ʱ����Ҫ�������������һ���������ڵ����ֵ��һ����������ô����ƫ����1���ػ����൱�ڶ��ϲ�ͼƬ����һ��ѹ����������������������ʱ�봫ͳ�ķ�����ʽ��ͬ���Ӿ������feature_map������ǰһ��ʱ������ǰ��ʱ��ͨ������������������õ���feature_map�����Է����봫ͳ��Ҳ��һ������Ҫ���¾����˵IJ������������ǽ���һ�³ػ���;�����������������ġ�
�����ڽ���֮ǰ�����Ȼع�һ�´�ͳ�ķ���������
����1.ͨ��ǰ������ÿһ�������ֵ$net_{i,j}$ (��������feature_map�ĵ�һ����Ԫ�����룺$net_{i_{11}}$)
����2.��������ÿ����Ԫ�������$\delta_{i,j}$ ��$\delta_{i,j} = \frac{\partial E}{\partial net_{i,j}}$������EΪ��ʧ��������õ���������������ƽ��������صȱ�ʾ��
����3.����ÿ����ԪȨ��$w_{i,j}$ ���ݶȣ�$\eta_{i,j} = \frac{\partial E}{\partial net_{i,j}} \cdot \frac{\partial net_{i,j}}{\partial w_{i,j}} = \delta_{i,j} \cdot out_{i,j}$
����4.����Ȩ�� $w_{i,j} = w_{i,j}-\lambda \cdot \eta_{i,j}$(����$\lambda$Ϊѧϰ��)
����������ķ���
������ǰ���ɵã�
\begin{equation}
\begin{aligned}
\ net_{o_{11}}&= conv (input,filter)\\
&= i_{11} \times h_{11} + i_{12} \times h_{12} +i_{21} \times h_{21} + i_{22} \times h_{22}\\
out_{o_{11}} &= activators(net_{o_{11}}) \\
&=max(0,net_{o_{11}})
\end{aligned}
\end{equation}
����������һ������Ҳ������һ������룬����$out_{i_{11}} = activators(net_{i_{11}}) = i_{11}$
�������ȼ��������������$\delta_{11}$��
$$\delta_{11} = \frac{\partial E}{\partial net_{o_{11}}} =\frac{\partial E}{\partial i_{11}} \cdot \frac{\partial i_{11}}{\partial net_{i_{11}}}$$(ע��������$net_{i_{11}}$,����������һ������룬����$net_{o_{11}}$)
�����ȼ���$\frac{\partial E}{\partial i_{11}} $
�����˴����Dz������$\frac{\partial E}{\partial i_{11}}$��ô�㣬�ǿ����Ȱ�input��ͨ������������������������feature_mapд����:
��
 �������
�������

![[���ѧϰ]ʵ��һ�������͵�AI���������忪ʼ��1�� - xerwin](/upload8/allimg/171115/1202222B9_lit.png)
 ���ʵ���
���ʵ��� ������Ѷ
������Ѷ ��ע����
��ע����
