Html5 canvas画图教程15：画扇形_H5之家 - 中国HTML5教程资源分享第一站

画扇形这个事儿，貌似不应该拖到现在讲，因为这明显跟前面几章“画圆形，画矩形”是一路的，但我拖到现在才讲是有理由的，因为画扇形需要用到我上两章讲的知识。

扇形，就是一个不完整的圆，提到圆，我们就能马上想到用arc方法来画。的确，arc可以画出扇形的弧线，但光是靠arc我们是不能画出扇形的，下面是一个扇形和一个不完整的圆弧：

抱歉，画得很粗略，但他们的区别还是很容易就看出来了。

如果我们不使用上两章讲的画面位移旋转与还原，那么画扇形就会让人头大无比。一个扇形，包含圆心，半径，起始与终止的角度，最后还要从圆心分别连接到起止点才行。

我先写一个初步的画扇形的函数：

	
						//扇形

						CanvasRenderingContext2D.prototype.sector = function (x, y, radius, sDeg, eDeg) {

						// 初始保存

						this.save();

						// 位移到目标点

						this.translate(x, y);

						this.beginPath();

						// 画出圆弧

						this.arc(0,0,radius,sDeg, eDeg);

						// 再次保存以备旋转

						this.save();

						// 旋转至起始角度

						this.rotate(eDeg);

						// 移动到终点，准备连接终点与圆心

						this.moveTo(radius,0);

						// 连接到圆心

						this.lineTo(0,0);

						// 还原

						this.restore();

						// 旋转至起点角度

						this.rotate(sDeg);

						// 从圆心连接到起点

						this.lineTo(radius,0);

						this.closePath();

						// 还原到最初保存的状态

						this.restore();

						return this;

						}

代码中已经有详细注释，但我还要说几句。函数中画路径的时候，就先画弧线，再从终点连到圆心，再从圆心连到起点。为什么？因为这个顺序路径才不会断——arc是从起点开始画起的，最后路径又回到起点，才合情合理。在测试函数的时候，我想当然的先画了弧线，再从起点连圆心连终点，结果导致路径断了。大家一定要注意。

此函数是附加于原型的，所以大家使用时可以这么用：

	
						var ctx = document.getElementById('cvs').getContext('2d');

						ctx.sector(100,100,50,0,Math.PI/180*230).fill();

这样你就能画出如下的扇形：

此函数写得比较粗略，以后可能会改进。也希望你能提出意见。

下面我们用上面的画扇形函数来画一个分饼统计图吧：

	
						var deg = Math.PI/180;

						ctx.sector(100,100,80,30*deg,111*deg).fill();

						ctx.fillStyle="#f00";

						ctx.sector(100,100,80,111*deg,190*deg).fill();

						ctx.fillStyle="#0f0";

						ctx.sector(100,100,80,190*deg,233*deg).fill();

						ctx.fillStyle="#00f";

						ctx.sector(100,100,80,233*deg,280*deg).fill();

						ctx.fillStyle="#789";

						ctx.sector(100,100,80,280*deg,345*deg).fill();

						ctx.fillStyle="#abcdef";

						ctx.sector(100,100,80,345*deg,30*deg).fill();

最终效果如图所示：

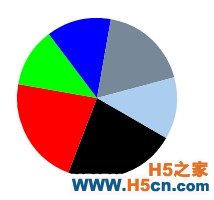
当然，实际上你可以用一个循环来搞定这个饼图，因为他们的位置，半径都是一样的，只是起止点不同。

大家可以思考一下不用位移与旋转的画法，不过真的是有点蛋疼。