最近开始学习Canvas,因为之前没有接触过，所以想找点东西练下手，写写动画。

突然想起之前看过 TQ大神 写的一篇 拖拽粘性小红球Canvas实现 ，重新翻出来看看。顺便用自己的语言重新书写了一遍。写篇文章记录下今天的学习过程。

先贴上效果预览二维码，或者点击查看

Canvas

Canvas不是什么新鲜的技术了，然而开始写相关代码就在昨天。

Canvas其实就是块画布，如果你学过 MFC的话，你会发现其实很多内容都是相同的。

// 获取画布
var canvas = document.getElementById('canvas');
// 2d画布
var ctx = canvas.getContext('2d');
// 填充矩形（x, y, width, height）
ctx.fillRect(x, y, width, height);
ctx.clearRect(x, y, width, height);
ctx.strokeRect(x, y, width, height);

绘制多边形可以使用路径

...
ctx.beginPath();
ctx.closePath();
// 移动画笔
ctx.moveTo(x, y);
// 画线
ctx.lineTo(x, y);
// 填充，描边
ctx.stroke();
ctx.fill();

绘制弧形，曲线

// 绘制规则弧形
ctx.arc(x, y, radius, startAngle, endAngle, clockwise)
// 二阶贝塞尔
ctx.quadraticCurveTo(cp1x, cp1y, x, y)
// 三阶贝塞尔
ctx.bezierCurveTo(cp1x, cp1y, cp2x, cp2y, x, y)

绘制图形常用的就这些了，还有就是注意Canvas坐标轴原点在左上角，角度使用的是弧度(希望你跟我一样忘了什么是弧度)。

三角含树

上次谈起这个沉重的话题应该是高等数学期末考。

但是不要慌! 记住几个常见的公式定理，其他的靠猜就行了。

A + B + C = 180. 正弦定理 a / sin A = b / sin B = c / sin C 余弦定理 c^2 = a^2 + b^2 - 2abcos C

维基百科

开始敲代码

为了让动画能够流畅，这里使用了 requestAnimationFrame 。

一步一步来。

function init() {
// 监听事件
addEventListener();
// 启动 requestAnimationFrame
requestAnimationFrame(loop);
}

监听三个事件，并只在事件监听中改变状态值，绘制图形放在loop中。

function touchstart(event) {
event.preventDefault();
isDragging = true;
mousePos.x = event.touches[0].pageX;
mousePos.y = event.touches[0].pageY;
...
}
function touchmove(event) {
...
}
function touchend() {
...
}
function addEventListener() {
window.addEventListener('touchstart', touchstart);
window.addEventListener('touchmove', touchmove);
window.addEventListener('touchend', touchend);
}
function loop() {
// 清除画板，重新绘制
ctx.clearRect(0, 0, width, height);
calPos();
changeSize();
drawBall();
drawDragBall();
// 贝塞尔曲线
drawBezier();
requestAnimationFrame(loop);
}
贝塞尔曲线

我们需要获取先获取两个圆的四个切点，因为都是直角，难度不大。

可以结合图看代码。

angle = Math.atan((centerPos.x - mousePos.x)/(centerPos.y - mousePos.y));
// 小三角形的两条边
var y = drawRadius * Math.sin(angle);
var x = Math.sqrt(Math.pow(drawRadius, 2) - Math.pow(y, 2));
y1 = centerPos.y - y;
x1 = centerPos.x + x;
y2 = centerPos.y + y;
x2 = centerPos.x - x;
y3 = mousePos.y - y;
x3 = mousePos.x + x;
y4 = mousePos.y + y;
x4 = mousePos.x - x;

再看图确保你知道贝塞尔曲线如何工作。

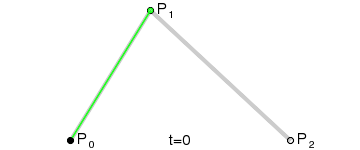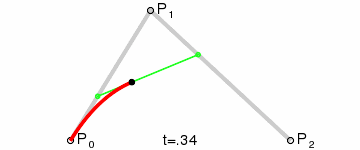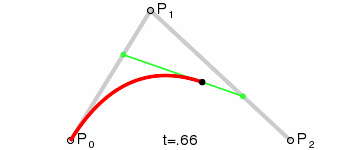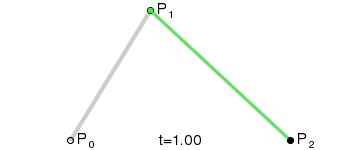
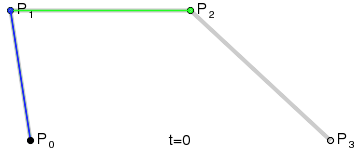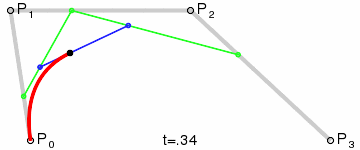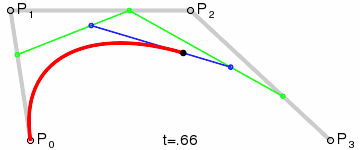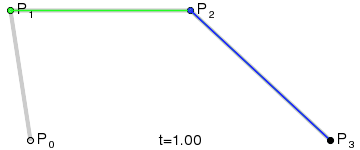
这里以两个圆心的中点为贝塞尔曲线的控制点

// 考虑到 控制点可能变动，所以这里算了两次
cx1 = (x1 + x4) / 2;
cy1 = (y1 + y4) / 2;
cx2 = (x2 + x3) / 2;
cy2 = (y2 + y3) / 2;
ctx.beginPath();
ctx.moveTo(x1,y1);
ctx.quadraticCurveTo(cx1, cy1, x3,y3);
ctx.lineTo(x4,y4);
ctx.quadraticCurveTo(cx2, cy2, x2,y2);
ctx.lineTo(x1,y1);
ctx.fillStyle = '#ea6d9e';
ctx.fill();
收尾动画

为了不让小球回弹的时候略显尴尬，这里用了 TWEEN.js 做收尾动画,在手指移开屏幕的时候触发。

function touchend() {
isDragging = false;
// 选择缓动函数
var bounce_animate_type = TWEEN.Easing.Elastic.Out;
// 调用Tween.js，声明开始和结束位置。
tween = new TWEEN.Tween(mousePos)
.to(centerPos, bounceTime)
.easing(bounce_animate_type)
.onUpdate(function() {
calDistance();
})
.onComplete(function() {
dragEnd = true;
cancelAnimationFrame(bounceTimer);
})
.start();
bounce();
}
function bounce(time) {
// drawRadius = ballRadius;
bounceTimer = requestAnimationFrame(bounce);
TWEEN.update(time);
}

主要代码就这些了， 最终代码 - github

再次感谢TQ 的教程。